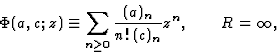Fonctions d'une variable complexe
Sommaire
Retour
page maths
Continuité, dérivabilité
et holomorphie
On note 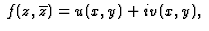 une fonction des variables complexes z=x+iy et
une fonction des variables complexes z=x+iy et 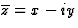 .
A noter que u (resp. v) est la partie réelle (resp.
imaginaire) de f. Une fonction f est une application
qui en tout point
.
A noter que u (resp. v) est la partie réelle (resp.
imaginaire) de f. Une fonction f est une application
qui en tout point 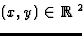 prend une valeur et une seule.
Retour sommaire Retour
page Maths
prend une valeur et une seule.
Retour sommaire Retour
page Maths
Théorème de Cauchy-Riemann
Si u(x,y) et v(x,y) sont différentiables
en (x,y) au point (x0,y0)
et si les conditions de Cauchy-Riemann
|
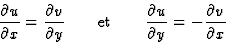 |
(1) |
sont satisfaites en (x0,y0) alors f
est 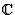 -dérivable
en z0 et
-dérivable
en z0 et 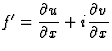 .
.
Remarques :
Sténographie : on définit la différentielle complexe
par
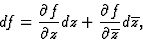
et par identification on obtient
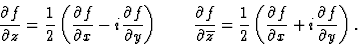
Les conditions (nécessaires) de Cauchy-Riemann s'écrivent
alors

Retour sommaire Retour
page Maths
Exemples de fonctions holomorphes
Exemples élémentaires :

Si f et g sont holomorphes dans un ouvert U alors
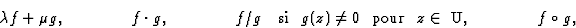
sont holomorphes dans U, avec les formules de dérivation évidentes.
Retour sommaire Retour
page Maths
Intégrale de Cauchy
On définit un chemin d'intégration 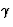 par la paramétrisation
par la paramétrisation 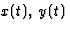 sous l'hypothèse que x(t) et y(t) soient
continues et à dérivées premières continues
pour
sous l'hypothèse que x(t) et y(t) soient
continues et à dérivées premières continues
pour ![$\, t\in[a,b]\,$](img25-7.gif) .
Alors pour
.
Alors pour 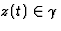 on a
on a

Soit f(z)=u(x,y)+iv(x,y)
une fonction 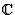 -continue
pour
-continue
pour 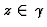 ;
on définit son intégrale de Cauchy le long du chemin
;
on définit son intégrale de Cauchy le long du chemin 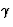 par
par
+i\dot{y}(t))dt.\end{displaymath}](img29-7.gif)
Avec les hypothèses faites, cette intégrale de Riemann en
variable t existe.
Ses propriétés les plus importantes sont :
Inégalité fondamentale :
Soit un chemin 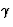 de longueur
de longueur 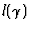 et soit
et soit 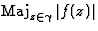 un majorant uniforme de |f(z)|, c'est-à-dire
qui ne dépend pas du point z choisi sur
un majorant uniforme de |f(z)|, c'est-à-dire
qui ne dépend pas du point z choisi sur 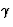 .
Alors on a
.
Alors on a
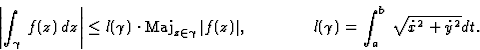
Retour sommaire Retour
page Maths
Théorème
de Cauchy
Ce théorème fondamental s'énonce : soit f(z)
holomorphe dans un ouvert simplement connexe U et soit 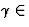 U un circuit de Jordan, alors on a
U un circuit de Jordan, alors on a
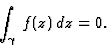
Remarques :
-
On ne peut rien conclure si f n'est pas holomorphe à l'intérieur
de
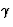 .
.
-
L'orientation de
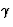 est sans importance.
est sans importance.
Retour sommaire Retour
page Maths
Notion de primitive
Soit f(z) holomorphe dans un ouvert U. On considère
2 chemins 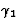 et
et 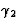 strictement contenus dans U, avec la même origine A et la même
extrêmité B et orientés de A vers B. Le théorème
de Cauchy implique
strictement contenus dans U, avec la même origine A et la même
extrêmité B et orientés de A vers B. Le théorème
de Cauchy implique
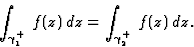
On peut, pour tout z et z0 dans U définir
la primitive
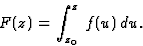
D'après ce qui précède elle est indépendante
du chemin (strictement contenu dans U) qui joint z et z0.
Elle est holomorphe pour 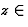 U et sa dérivée est F'(z)=f(z).
U et sa dérivée est F'(z)=f(z).
Retour sommaire Retour
page Maths
Relations intégrales de
Cauchy
Soit f(z) holomorphe dans l'ouvert U contenant 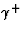 .
Pour tout z dans un ouvert D intérieur à
.
Pour tout z dans un ouvert D intérieur à 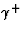 toutes les dérivées f(n)(z)
sont holomorphes dans D
toutes les dérivées f(n)(z)
sont holomorphes dans D U et on a les relations intégrales de Cauchy
U et on a les relations intégrales de Cauchy
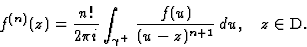
Remarques :
-
Attention à l'orientation positive de
 .
.
-
Pour n=0 on en tire la relation de la moyenne
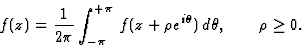
Retour sommaire Retour
page Maths
Théorèmes de Morera
et Liouville
Théorème de Morera : soit f continue
dans un ouvert simplement connexe U; si pour tout circuit 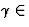 U on a
U on a 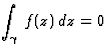 alors f est holomorphe dans U.
alors f est holomorphe dans U.
Théorème de Liouville : si f est holomorphe-entière
et bornée à distance finie et à l'infini, alors c'est
une constante.
Remarques :
-
On en déduit, par un raisonnement par l'absurde, le théorème
de d'Alembert : tout polynôme de degré n possède n
racines (comptées avec leur multiplicité) dans
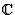 .
.
-
La fonction eiz est holomorphe-entière.
Son module est borné si Im
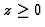 mais pas si Im
mais pas si Im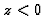 .
.
Retour sommaire Retour
page Maths
Théorème de Weierstrass
Soit la série  dont la somme sera notée S(z). Sous les hypothèses
:
dont la somme sera notée S(z). Sous les hypothèses
:
-
Pour
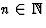 les fn(z) sont holomorphes dans un domaine fermé
simplement connexe D dont le bord est un circuit de Jordan
les fn(z) sont holomorphes dans un domaine fermé
simplement connexe D dont le bord est un circuit de Jordan 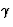 ,
,
-
La série converge uniformément
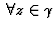 ,
,
on a le théorème de Weierstrass:
-
S(z) est holomorphe dans D,
-
Ses dérivées sont données par
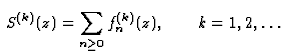 .
.
Retour sommaire Retour
page Maths
Séries entières
Soit la série entière 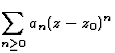 ,
de rayon de convergence R (cf les notes de cours sur les séries
pour les définitions).
,
de rayon de convergence R (cf les notes de cours sur les séries
pour les définitions).
Théorème : la somme S(z) d'une série
entière est holomorphe si |z-z0|<R
où R est le rayon de convergence de la série entière
et ses dérivées successives s'obtiennent en dérivant
terme à terme.
Analyticité : on dit que f(z) est analytique
en z0 si on peut la développer en série
entière dans un voisinage fini de z0. Le théorème
précédent montre que l'analyticité en z0
entraîne l'holomorphie en z0.
Retour sommaire Retour
page Maths
Série de Taylor
Toute fonction f(z) holomorphe dans un ouvert U est développable
en série de Taylor (c'est une série entière...), d'une
façon unique, en tout point 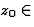 U avec :
U avec :
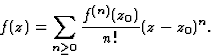
Il en résulte que l'holomorphie en un point implique l'analyticité
en ce point. En combinant ce résultat avec celui de la section 10
on en conclut à l'équivalence des notions d'holomorphie et
d'analyticité.
Exemple : la fonction 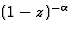 est analytique dans
est analytique dans 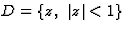 .
Elle est donc développable en série de Taylor autour de tout
point
.
Elle est donc développable en série de Taylor autour de tout
point 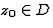 .
En particulier autour de z0=0 on a la série binômiale
généralisée
.
En particulier autour de z0=0 on a la série binômiale
généralisée
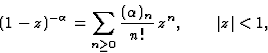
avec la définition
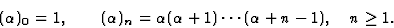
Pour 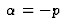 avec
avec 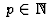 on retrouve la formule du binôme.
on retrouve la formule du binôme.
Retour sommaire Retour
page Maths
Série
de Laurent
Soit f(z) analytique dans la couronne ouverte 0<|z-z0|<R,
alors elle est développable, de façon unique, en série
de Laurent
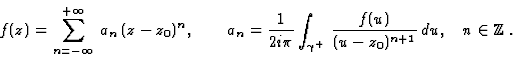
Attention : le circuit de Jordan 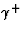 doit être pris à l'intérieur de la région d'analyticité
de f, c'est-à-dire la couronne ouverte 0<|z-z0|<R.
doit être pris à l'intérieur de la région d'analyticité
de f, c'est-à-dire la couronne ouverte 0<|z-z0|<R.
Le résidu de f en z0 est défini
par
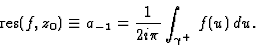
Retour sommaire Retour
page Maths
-
Classification
des singularités isolées:
On peut avoir :
Exemple : z=0 est un point singulier essentiel pour 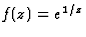 et dans la couronne ouverte |z|>0 on a la série de Laurent
et dans la couronne ouverte |z|>0 on a la série de Laurent 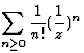 .
.
Remarque : Attention aux singularités apparentes, qui
sont des points d'analyticité... Par exemple le point z=0
pour la fonction 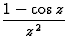 .
.
Retour sommaire Retour
page Maths
En un pôle simple on a
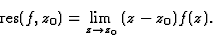
Parfois il est plus commode d'écrire
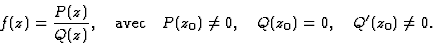
Ces conditions assurent que z0 est un pôle simple.
Alors le résidu est donné par
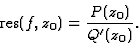
Pour un pôle d'ordre 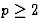 on a
on a
![\begin{displaymath}\displaystyle \mbox{res}(f,z_0)=\lim_{z\to z_0}\left\{\frac ... ...\frac{d^{p-1}}{dz^{p-1}}\left[(z-z_0)^p\, f(z)\right]\right\}.\end{displaymath}](img88.gif)
Remarque : Pour calculer un résidu il est toujours possible de
revenir à la définition (calculer le coefficient a-1
de sa série de Laurent). En un point singulier essentiel c'est la
seule méthode possible.
Retour sommaire Retour
page Maths
Théorème des résidus
Soit f(z) analytique à l'intérieur d'un circuit
de Jordan 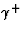 ,
sauf en un nombre fini de singularités isolées
,
sauf en un nombre fini de singularités isolées 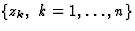 .
Alors on a
.
Alors on a
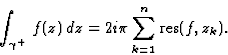
Remarques importantes :
-
Seules les singularités intérieures à
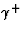 contribuent à l'intégrale.
contribuent à l'intégrale.
-
Noter que
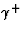 est orienté positivement.
est orienté positivement.
Lemme utile :
Soit 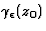 l'arc de cercle d'angle au sommet
l'arc de cercle d'angle au sommet 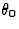 défini par
défini par 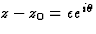 avec
avec ![$\theta\in[0,\theta_0]$](img94.gif) .
Alors si z0 est un pôle simple de f(z)
on a la relation
.
Alors si z0 est un pôle simple de f(z)
on a la relation
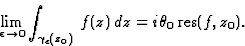
Retour sommaire Retour
page Maths
Application au calcul de certaines
séries
On se propose de calculer les séries
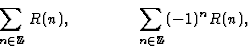
où R(z) est une fraction rationnelle telle que si  son module soit
son module soit 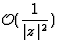 .A
chacune des séries on associe les fonctions auxiliaires
.A
chacune des séries on associe les fonctions auxiliaires
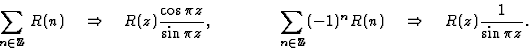
On a les théorèmes :

où la somme porte sur toutes les singularités.
Exemples : la somme 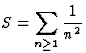 se calcule avec la fonction auxiliaire
se calcule avec la fonction auxiliaire 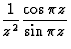 .
Il faut faire attention que les points
.
Il faut faire attention que les points 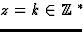 sont des pôles simples alors que z=0 est un pôle triple.
On obtient
sont des pôles simples alors que z=0 est un pôle triple.
On obtient 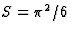 .
.
La fonction auxiliaire 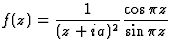 donne les séries
donne les séries
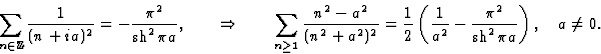
Retour sommaire Retour
page Maths
Equations différentielles
linéaires du second ordre
On les écrira sous la forme
|
y''(z)+p(z)y'(z)+q(z)y(z)=0. |
(2) |
Le changement de fonction
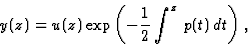
permet de ramener l'équation de départ à la forme
canonique :
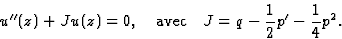
Le point z0 est un point ordinaire de l'équation
différentielle (2)
si p et q sont analytiques en z0.
En un point ordinaire on a le théorème d'existence et d'unicité
:
-
Il existe une solution de (2)
analytique en z0.
-
Si l'on se donne y(z0) et y'(z0),
alors la solution de l'équation (2)
est unique.
-
Points singuliers
réguliers
Le point z0 est un point singulier régulier de
l'équation différentielle (2)
si, en écrivant
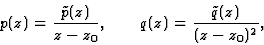
les fonctions 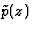 et
et 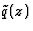 sont analytiques en z0.
sont analytiques en z0.
En ces points on peut chercher une solution sous la forme d'une série
de Frobenius
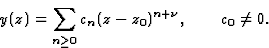
Les valeurs possibles pour 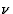 sont les solutions de l'équation indicielle
sont les solutions de l'équation indicielle
|
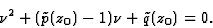 |
(3) |
On peut montrer que pour un point singulier régulier la série
entière 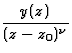 a toujours un rayon de convergence fini. Cependant, si la différence
des racines de l'équation (3)
est un entier relatif il est possible que la méthode ne donne
pas 2 solutions linéairement indépendantes...
a toujours un rayon de convergence fini. Cependant, si la différence
des racines de l'équation (3)
est un entier relatif il est possible que la méthode ne donne
pas 2 solutions linéairement indépendantes...
Exemple 1 : les fonctions de Bessel
Ce sont les solutions de l'équation
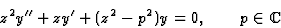
Le point singulier z0=0 est régulier (ici 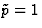 et
et 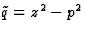 )
et l'équation indicielle a pour solutions
)
et l'équation indicielle a pour solutions 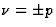 .
Pour
.
Pour  on obtient 2 solutions linéairement indépendantes avec le
comportement
on obtient 2 solutions linéairement indépendantes avec le
comportement
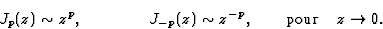
La différence des indices est 2p, cependant si p est
demi-entier on peut montrer que la méthode de Frobenius donne 2
solutions linéairement indépendantes, alors que si p
est un entier on a la relation J-p(z)=(-1)pJp(z)
qui montre que J-p et Jp ne
sont pas linéairement indépendantes. En fait la solution
linéairement indépendante de Jp pour p
entier positif a un point de branchement de type 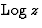 en z=0 qui ne peut être obtenu par une série de Frobenius!
en z=0 qui ne peut être obtenu par une série de Frobenius!
Exemple 2 : la fonction hypergéométrique confluente
Soit l'équation différentielle
L'équation indicielle a pour racines 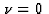 et
et 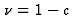 .
Dans ce qui suit on considère
.
Dans ce qui suit on considère 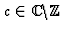 .
La série de Frobenius correspondant à
.
La série de Frobenius correspondant à 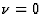 donne la fonction hypergéométrique confluente
donne la fonction hypergéométrique confluente 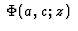 définie par
définie par
|
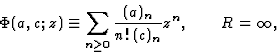 |
(5) |
qui est analytique-entière.
La série de Frobenius correspondant à 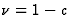 est alors
est alors
|
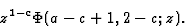 |
(6) |
A noter que ces deux solutions ne sont distinctes et bien définies
que pour 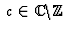 .
.
-
Points singuliers
irréguliers
Ce sont tous les points singuliers qui ne sont pas réguliers...
Exemple : le point 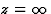 pour l'équation de Bessel. Si l'on pose u=1/z l'équation
différentielle devient
pour l'équation de Bessel. Si l'on pose u=1/z l'équation
différentielle devient
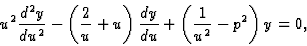
et u=0, donc 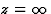 est un point singulier irrégulier.
est un point singulier irrégulier.
On peut vérifier que l'équation différentielle
satisfaite par l'hypergéométrique confluente a aussi 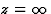 comme point singulier irrégulier.
comme point singulier irrégulier.
Le point à l'infini n'est pas toujours un point singulier irrégulier
comme le montre l'exemple
z(1-z)y''+(c-(a+b+1)z)y'-aby=0,
pour lequel les points 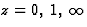 sont des points singuliers réguliers.
sont des points singuliers réguliers.
On définit le Wronskien de deux fonctions par
W[y1,y2]=y1y2'-y1'y2.
Ses propriétés les plus utiles sont :
-
Il est bilinéaire en y1 et y2.
-
Il est antisymétrique : W[y1,y2]=-W[y2,y1].
-
On a l'équivalence
![\begin{displaymath}W[y_1,y_2]=0\qquad\Leftrightarrow\qquad y_1\quad\mbox{et}\quad y_2\quad\mbox{ sont lin\'eairement d\'ependantes.}\end{displaymath}](img135.gif)
-
Si y1 et y2 sont deux solutions de
l'équation différentielle (2)
alors leur Wronskien W[y1,y2]
est solution de l'équation différentielle du premier ordre
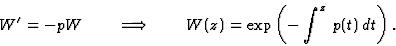
Exemple : pour les solutions de l'équation différentielle
(4)
le Wronskien est 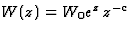 ,
et un calcul au voisinage de z=0 donne
,
et un calcul au voisinage de z=0 donne 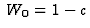 ,
confirmant l'indépendance linéaire des solutions (5)
et (6).
,
confirmant l'indépendance linéaire des solutions (5)
et (6).
Retour sommaire Retour
page Maths
![]() si lorsque
si lorsque ![]() alors
alors ![]() .C'est
équivalent à la continuité de u(x,y)
et de v(x,y) considérées comme fonctions
des 2 variables réelles x et y.
.C'est
équivalent à la continuité de u(x,y)
et de v(x,y) considérées comme fonctions
des 2 variables réelles x et y.
![]() -dérivable
en z0 si
-dérivable
en z0 si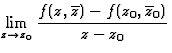 existe. On note cette limite f'. Observer le rôle privilégié
que joue la variable z.
existe. On note cette limite f'. Observer le rôle privilégié
que joue la variable z.
![]() -dérivable
dans un voisinage ouvert de z0. Par extension on parlera
d'holomorphie dans un ouvert U si f est holomorphe en tout point
de l'ouvert U.
-dérivable
dans un voisinage ouvert de z0. Par extension on parlera
d'holomorphie dans un ouvert U si f est holomorphe en tout point
de l'ouvert U.
![]() on aboutirait au concept de fonction anti-holomorphe.
on aboutirait au concept de fonction anti-holomorphe.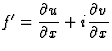 .
.

+i\dot{y}(t))dt.\end{displaymath}](img29-7.gif)
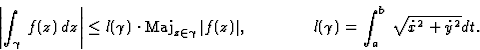
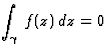 alors f est holomorphe dans U.
alors f est holomorphe dans U.
 dont la somme sera notée S(z). Sous les hypothèses
:
dont la somme sera notée S(z). Sous les hypothèses
:
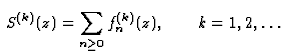 .
.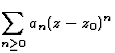 ,
de rayon de convergence R (cf les notes de cours sur les séries
pour les définitions).
,
de rayon de convergence R (cf les notes de cours sur les séries
pour les définitions).
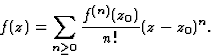
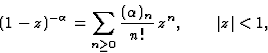
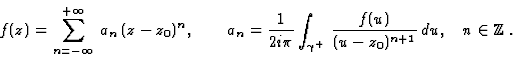
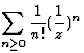 .
.
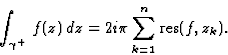
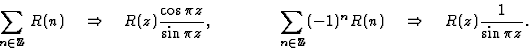
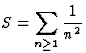 se calcule avec la fonction auxiliaire
se calcule avec la fonction auxiliaire 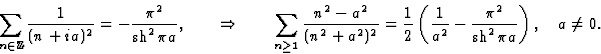
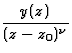 a toujours un rayon de convergence fini. Cependant, si la différence
des racines de l'équation (
a toujours un rayon de convergence fini. Cependant, si la différence
des racines de l'équation (