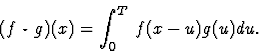Séries de Fourier
Sommaire :
Séries de Fourier complexes
Soit f(x) une fonction à valeurs complexes. Sa période
est définie comme la plus petite valeur T, avec 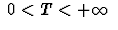 telle que :
telle que :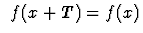 .
On définit ses coefficients de Fourier
.
On définit ses coefficients de Fourier 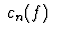 par
par
|
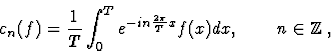 |
(1) |
et la série de Fourier (SF) associée à f(x)
est
|
 |
(2) |
Afin de préciser le sens de cette somme infinie de fonctions, et
son lien éventuel avec f(x), on considère la
suite des sommes partielles
|
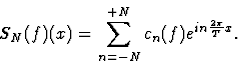 |
(3) |
Remarques :
-
La SF et la suite
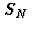 ont pour période T, comme f(x).
ont pour période T, comme f(x).
-
Du fait de la périodicité de f(x) on peut prendre,
dans la relation (1),
des bornes
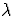 et
et 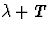 pour tout
pour tout 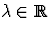 .
.
-
L'égalité éventuelle entre f(x)
et la limite lorsque
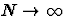 de
de 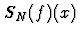 ne va pas de soi! Il faut préciser la notion de convergence considérée
: simple, uniforme, en norme, etc...
ne va pas de soi! Il faut préciser la notion de convergence considérée
: simple, uniforme, en norme, etc...
On a les propriétés simples :
Séries de Fourier réelles
Si f(x) est réelle on peut définir
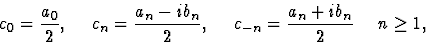
avec des coefficients 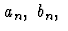 réels. La relation (1)
donne
réels. La relation (1)
donne
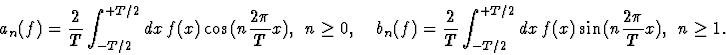
Cette écriture est adaptée au cas où f(x)
a une parité définie. La série de Fourier (2)
s'écrit alors
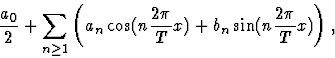
avec la suite des sommes partielles
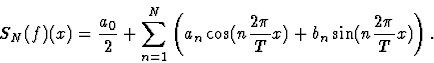
parité :
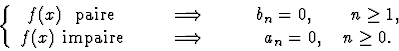
Sommaire Retour
page Maths
Lien entre séries
de Laurent et séries de Fourier
Soit f(z) une fonction analytique dans la couronne ouverte 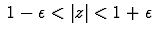 avec
avec 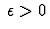 .
On a vu qu'alors f(z) est développable en série
de Laurent
.
On a vu qu'alors f(z) est développable en série
de Laurent
|
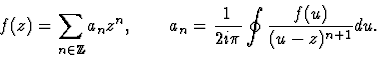 |
(4) |
Si l'on pose 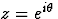 la série de Laurent devient une SF
la série de Laurent devient une SF
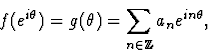
avec 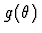 de période
de période 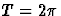 .La
relation (4)
devient
.La
relation (4)
devient
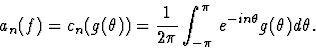
Avec les hypothèses faites la SF converge absolument et uniformément
vers 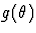 pour tout
pour tout 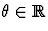 .
.
Cette approche est trop restrictive car on veut étudier
les SF de fonctions d'une variable réelle. Celles-ci ne sont pas
en général prolongeables en des fonctions analytiques dans 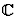 .
.
Sommaire Retour
page Maths
Fonctions absolument continues
On dit que f(x) est absolument continue pour ![$x\in[a,b]$](img32-6.gif) si pour toute famille d'intervalles 2 à 2 disjoints
si pour toute famille d'intervalles 2 à 2 disjoints ![$[a_k,b_k],\ \ b_k\gt a_k$](img33-6.gif) avec
avec 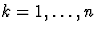 on a
on a
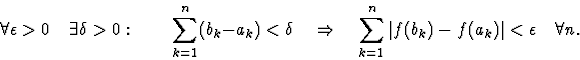
Pour n=1 il en résulte que la continuité absolue implique
la continuité uniforme (donc une fonction qui n'est pas continue
ne peut être absolument continue).
On a le très important résultat, spécifique de
l'intégrale de Lebesgue :
Théorème : soit 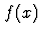 localement sommable (c. a. d. que sur tout compact
localement sommable (c. a. d. que sur tout compact ![${\mathbb K}\subset[a,b]$](img37-5.gif) on a
on a  )
alors la fonction
)
alors la fonction
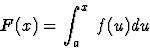
est absolument continue si ![$x\in[a,b]$](img32-6.gif) .
.
Avec ces notions on peut énoncer la relation d'intégration
par parties :
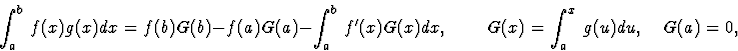
valable si g(x) est localement sommable et f(x)
absolument continue.
Sommaire Retour
page Maths
Convergences des SF
Sommaire Retour
page Maths
Convergence simple
Soit f(x) réelle de période T, avec
un nombre fini de discontinuités finies dans la période,
et qui admet en tout point x0 une dérivée
à droite et à gauche. Alors la suite des sommes partielles
SN(f)(x0)
converge simplement (c. a. d. comme une série numérique)
lorsque  vers
vers
-
[
 ]
] 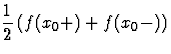 si x0 est un point de discontinuité de f,
si x0 est un point de discontinuité de f,
-
[
 ]
f(x0)
si f est continue en x=x0.
]
f(x0)
si f est continue en x=x0.
Remarques :
-
La seule continuité de f(x) n'implique pas la convergence
simple de la SF. Il existe des fonctions continues en un point et pour
lesquelles la SF diverge en ce point! L'hypothèse d'existence d'une
dérivée à gauche et à droite est une restriction
très forte. On sait qu'il existe des fonctions continues sur
 qui sont nulle part dérivables (voir l'exemple de Weierstrass page
351 de la référence [3]).
qui sont nulle part dérivables (voir l'exemple de Weierstrass page
351 de la référence [3]).
-
Si l'on suppose f(x) continue, peut-on resommer plus astucieusement
les sommes partielles de façon à reconstruire f(x)?
Le théorème de Fejér donne un réponse positive
à cette question. Soit f(x) périodique, de
période T, et continue
 ,
alors la suite des moyennes arithmétiques
,
alors la suite des moyennes arithmétiques
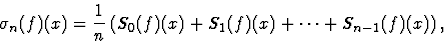 converge uniformément vers f(x) lorsque
converge uniformément vers f(x) lorsque 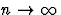 .
.
Convergence uniforme de la série
de Fourier
Soit f(x) de période T et absolument continue 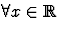 avec
avec 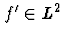 alors
alors 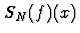 converge uniformément vers f(x) pour tout
converge uniformément vers f(x) pour tout 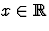 .
.
Convergence en norme L2
Si 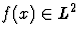 (c. a. d. si l'intégrale
(c. a. d. si l'intégrale 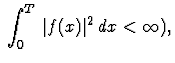 alors la suite SN(f)(x) converge en moyenne
quadratique vers f(x) ce qui signifie
alors la suite SN(f)(x) converge en moyenne
quadratique vers f(x) ce qui signifie
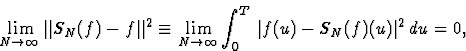
ou, de façon équivalente
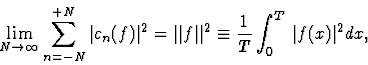
et aussi
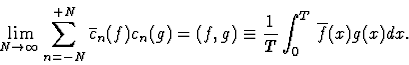
La dernière relation découle de la précédente
si l'on utilise l'identité dite de polarisation
4(f,g)=||f+g||2-||f-g||2+i||f-ig||2-i||f+ig||2.
Remarque : la convergence uniforme implique la convergence simple et
la convergence en norme L2.
Sommaire Retour
page Maths
Propriétés des
coefficients de Fourier
Sommaire Retour
page Maths
Lemme de Riemann-Lebesgue :
Soit 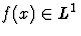 (c. a. d. que
(c. a. d. que 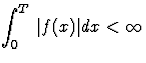 )
alors on a
)
alors on a
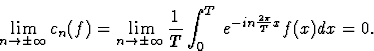
Du fait que 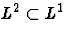 ce résultat reste vrai si
ce résultat reste vrai si 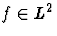 .
.
Théorème de nullité
:
Si 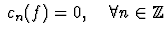 alors
f(x)
est presque partout nulle. Si de plus f(x) est continue
alors
alors
f(x)
est presque partout nulle. Si de plus f(x) est continue
alors 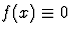 .
.
Décroissance pour 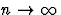 :
:
Si l'on veut préciser le comportement des cn il
faut faire des hypothèses supplémentaires. Par exemple :
si 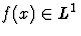 et si
et si 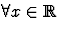 et
et 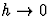 on a
on a
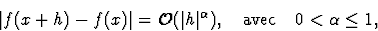
alors on a
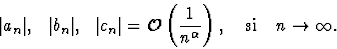
Dérivation terme à
terme :
Soit f(x) de période T et absolument continue
alors on a
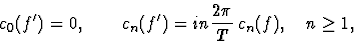
ou, en termes des coefficients réels
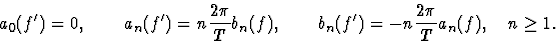
Convolution :
Soient f(x) et g(x) sommables sur la période
T.
On définit leur convolution par
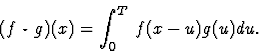
On a les propriétés :
Sommaire Retour
page Maths
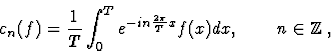

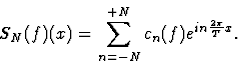
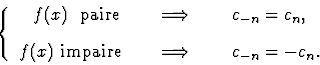
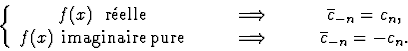
![]()
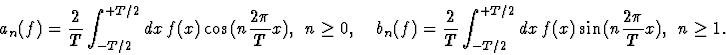
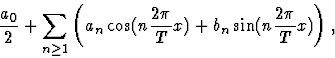
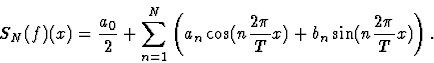
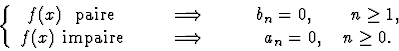
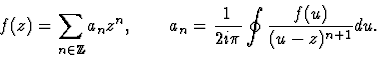
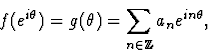
![]()
![]() .
.
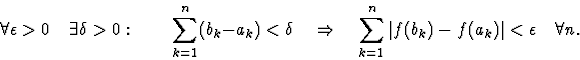
![]() localement sommable (c. a. d. que sur tout compact
localement sommable (c. a. d. que sur tout compact ![]() on a
on a  )
alors la fonction
)
alors la fonction
![]()
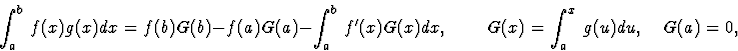
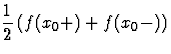 si x0 est un point de discontinuité de f,
si x0 est un point de discontinuité de f,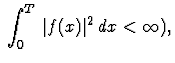 alors la suite SN(f)(x) converge en moyenne
quadratique vers f(x) ce qui signifie
alors la suite SN(f)(x) converge en moyenne
quadratique vers f(x) ce qui signifie
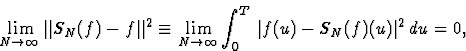
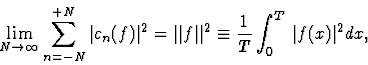
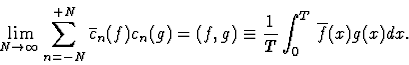
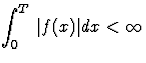 )
alors on a
)
alors on a
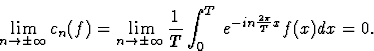
:
![]()
![]()
![]()
![]()