-Définitions
-Résultats
généraux
-Séries à
termes positifs
-Séries alternées
-Séries doubles
-Séries de
fonctions
-Séries entières
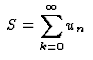 est défini comme la limite (si elle existe) de la suite des sommes
partielles :
est défini comme la limite (si elle existe) de la suite des sommes
partielles :
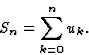
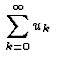 est convergente et a pour somme S.
est convergente et a pour somme S.
On dit que la série 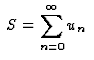 converge absolument si
converge absolument si 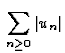 converge. La convergence absolue entraîne la convergence simple par
l'inégalité
converge. La convergence absolue entraîne la convergence simple par
l'inégalité
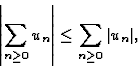
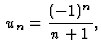 qui converge simplement mais pas absolument.
qui converge simplement mais pas absolument.
Sommaire sur les séries
Retour page Maths
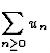 converge il est nécessaire que
converge il est nécessaire que 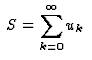 converge ssi la suite
converge ssi la suite ![]()
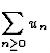 converge.
converge.
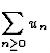 et
et 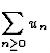 diverge alors
diverge alors 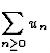 converge.
converge.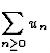 et
et 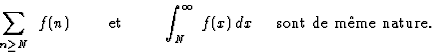
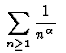 converge si
converge si 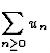 converge,
converge,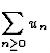 diverge.
diverge.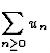 converge,
converge,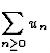 diverge.
diverge.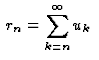 est majoré par
est majoré par 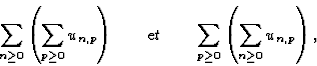
![]()
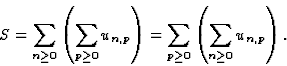
On dit que 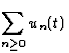 converge simplement en t=t0 vers S(t0)
si
converge simplement en t=t0 vers S(t0)
si
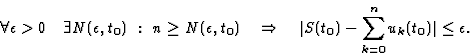
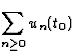 est une série numérique puisque t est fixé
à la valeur t0
est une série numérique puisque t est fixé
à la valeur t0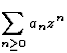 la série entière (centrée sur le point z=0).
On a les résultats :
la série entière (centrée sur le point z=0).
On a les résultats :
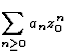 soit convergente, alors on sait que
soit convergente, alors on sait que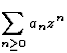 ,
de rayon de convergence R1, et
,
de rayon de convergence R1, et 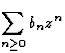 ,
de rayon de convergence R2, alors leur produit est une
série entière
,
de rayon de convergence R2, alors leur produit est une
série entière 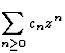 dont les coefficients sont donnés par
dont les coefficients sont donnés par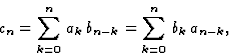
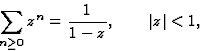
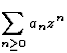 est nulle pour |z|<r avec
est nulle pour |z|<r avec